复数的加法

关于复数的加法，我们规定对于任意两个复数z1=a1+b1i(a1, b1∈R)和z2=a2+b2i(a2, b2∈R)，它们的和z1+z2=(a1+b1i)+(a2+b2i)=(a1+a2)+(b1+b2)i。

我们发现任意两个复数相加还是一个复数，并且复数的相加类似于多项式的相加，因此，对于任意z1，z2，z3∈C，我们可以得到：

z1+z2=z2+z1；

(z1+z2)+z3=z1+(z2+z3)。

上周我们讲了复数z可以表示为复平面中的一个向量，那么复数z1和复数z2的相加也可以看作是两个向量的相加，如图：

复数的减法

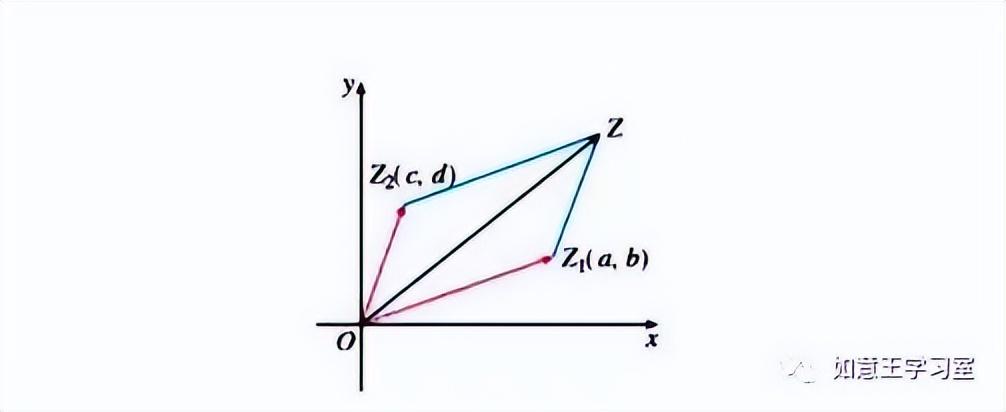
复数的减法是复数加法的逆运算，因此我们可以得到任意两个复数z1=a1+b1i(a1, b1∈R)和z2=a2+b2i(a2, b2∈R)，它们的差z1-z2=(a1+b1i)-(a2+b2i)=(a1-a2)+(b1-b2)i。

我们发现任意两个复数相减还是一个复数，并且也与多项式类似。

复数的乘法

关于复数的乘法，我们规定对于任意两个复数z1=a1+b1i(a1, b1∈R)和z2=a2+b2i(a2, b2∈R)，它们的积z1z2=(a1+b1i)(a2+b2i)=a1a2+b1a2i+a1b2i+b1b2i^2=a1a2+b1a2i+a1b2i-b1b2=(a1a2-b1b2)+(a1b2+b1a2)i。

我们发现任意两个复数相乘也还是一个复数，并且也与多项式类似，因此，对于任意z1，z2，z3∈C，我们可以得到：

z1z2=z2z1；

(z1z2)z3=z1(z2z3)；

z1(z2+z3)=z1z2+z1z3。

复数的除法

根据复数的乘法，我们可以得到对于任意两个复数z1=a1+b1i(a1, b1∈R)和z2=a2+b2i(a2, b2∈R)，z1/z2=(a1+b1i)/(a2+b2i)=[(a1+b1i)(a2-b2i)]/[(a2+b2i)(a2-b2i)]=[(a1a2+b1b2)+(b1a2-a1b2)i]/(c^2+d^2)=(a1a2+b1b2)/(c^2+d^2)+[(b1a2-a1b2)/(c^2+d^2)]i。

我们发现任意两个复数相除也还是一个复数。